แผ่นจารึกดินเหนียวขนาดเล็กนี้มีชื่อว่า Plimpton 322 ถูกค้นพบในช่วงต้นทศวรรษ 1900 ในสถานที่ซึ่งปัจจุบันเป็นบริเวณภาคใต้ของประเทศอิรัก ถูกค้นพบโดย Edgar Banks นักโบราณคดี นักการทูต และผู้ค้าวัตถุโบราณ ผู้ซึ่งเป็นแรงบันดาลใจและต้นแบบบุคลิกของพระเอกในภาพยนตร์ชื่อดังก้องโลก Indiana Jones
แผ่นจารึกนี้เชื่อว่าถูกเขียนขึ้นเมื่อราว 1800 ปีก่อนคริสต์ศักราช มีลักษณะเป็นตารางที่มี 4 คอลัมน์และ 15 แถว ในตารางเป็นตัวเลขที่เขียนด้วยอักษรรูปลิ่ม (Cuneiform script) ที่ใช้กันในยุคนั้น และได้สร้างความงุนงงสงสัยแก่นักวิจัยตลอดมาว่ามันถูกทำขึ้นเพื่อวัตถุประสงค์อะไร
Plimpton 322 ได้สร้างปริศนาให้แก่นักคณิตศาสตร์มานานกว่า 70 ปี ตั้งแต่ถูกเข้าใจว่ามันประกอบด้วยรูปแบบพิเศษของตัวเลขที่เรียกว่า “Pythagorean triples” Daniel Mansfield หนึ่งในทีมวิจัยกล่าว “ปริศนาสำคัญของมันคือวัตถุประสงค์ ทำไมอาลักษณ์ในสมัยโบราณจึงต้องทำงานที่ซับซ้อนด้วยการเขียนและจัดเรียงตัวเลขบนแผ่นจารึก”
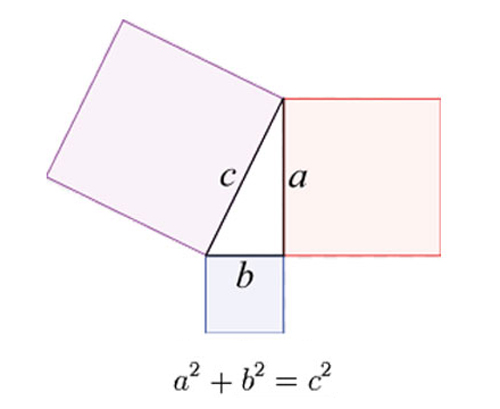
Pythagorean triples เป็นตัวเลข 3 ตัวที่สอดคล้องกับทฤษฎีสามเหลี่ยมมุมฉากของพีทาโกรัสนักคณิตศาสตร์คนสำคัญของโลกที่บอกว่า ผลรวมของค่ากำลังสองของความยาวด้านประกอบมุมฉากเท่ากับค่ากำลังสองของความยาวด้านตรงข้ามมุมฉาก หรือ a2 + b2 = c2 ตามรูปด้านล่าง เช่น 3, 4, 5 หรือ 5, 12, 13 เป็นต้น แต่ในแผ่นจารึกจะเป็นตัวเลขที่มีค่าค่อนข้างมาก แถวแรกของมันเป็นเลข 19, 120 และ 169
“งานวิจัยของเราได้แสดงให้เห็นว่าแผ่นจารึก Plimpton 322 ได้บรรยายรูปร่างของสามเหลี่ยมมุมฉากโดยการใช้ตรีโกณมิติแบบใหม่ที่ใช้อัตราส่วน ไม่ใช่มุมและวงกลม” Mansfield กล่าว “มันเป็นผลงานทางคณิตศาสตร์อันน่าทึ่งที่แสดงความอัจฉริยะอย่างไม่มีข้อสงสัย”
วิชาคณิตศาสตร์ของชาวบาบิโลนใช้ระบบเลขฐาน 60 แทนที่จะเป็นระบบเลขฐาน 10 ที่เราใช้กันในปัจจุบัน ด้วยการใช้แบบจำลองทางคณิตศาสตร์ของชาวบาบิโลน นักวิจัยสามารถแสดงให้เห็นว่าแผ่นจารึกดั้งเดิมมี 6 คอลัมน์และ 38 แถว พวกเขายังได้แสดงวิธีที่นักคณิตศาสตร์ในยุคนั้นใช้ระบบของชาวบาบิโลนให้ได้มาซึ่งตัวเลขบนแผ่นจารึก
นักวิจัยชี้ว่าแผ่นจารึกเป็นเครื่องมืออันทรงพลังที่สามารถใช้ในการสำรวจพื้นที่หรือการคำนวณทางสถาปัตย์เพื่อการก่อสร้างพระราชวัง วิหาร หรือพีระมิดขั้นบันได
แต่ถ้าหากงานวิจัยนี้ถูกต้องจะทำให้ Hipparchus นักดาราศาสตร์ชาวกรีกซึ่งมีชีวิตอยู่ราว 120 ปีก่อนคริสต์ศักราชจะมิใช่บิดาแห่งวิชาตรีโกณมิติตามที่เขาได้รับการยกย่องมาอย่างยาวนาน นักวิชาการระบุว่าอายุของแผ่นจารึกอยู่ในราว 1822-1762 ปีก่อนคริสต์ศักราช
แผ่นจารึก Plimpton 322 นอกจากจะเป็นตารางตรีโกณมิติที่เก่าแก่ที่สุดแล้วยังเป็นตารางตรีโกณมิติที่แม่นยำมากที่สุดอีกด้วย เหตุผลคือระบบเลขฐาน 60 มีการแบ่งส่วนย่อยที่แน่นอนมากกว่าระบบเลขฐาน 10 ซึ่งทำให้มีการปัดเศษน้อยกว่า ในระบบเลขฐาน 10 มีเลขเพียง 2 ตัวเท่านั้นที่หาร 10 ได้ลงตัวคือ 2 กับ 5 แต่สำหรับระบบเลขฐาน 60 มีมากกว่ากันเยอะ การมีส่วนย่อยที่มีค่าแน่นอนมากกว่าหมายถึงจะมีการประมาณการน้อยกว่า และนักวิจัยบอกว่าเราสามารถเรียนรู้จากมันได้แม้ในปัจจุบันนี้

“มันเข้ากันได้ดีกับโลกสมัยใหม่ในยุคปัจจุบัน” Mansfield กล่าว “วิชาคณิตศาสตร์ของชาวบาบิโลนอาจจะล้าสมัยมากกว่า 3,000 ปี แต่มันยังนำไปใช้งานได้ดีในการสำรวจ คอมพิวเตอร์กราฟฟิก และการศึกษา นี่เป็นตัวอย่างที่หายากยิ่งของโลกยุคโบราณที่ได้สอนในสิ่งใหม่แก่พวกเรา”
ข้อมูลและภาพจาก phys.org, sciencealert



