อัจฉริยภาพฉายแววตั้งแต่เยาว์วัย
ออยเลอร์เป็นชาวสวิสเกิดเมื่อปี 1707 ที่เมืองบาเซิลในครอบครัวของบาทหลวง พ่อเป็นบาทหลวง แม่เป็นลูกสาวของบาทหลวง ตัวเขาถูกตั้งความหวังให้เดินตามรอยพ่อสืบทอดการเป็นบาทหลวงต่อไป ออยเลอร์สนใจวิชาคณิตศาสตร์ตั้งแต่เด็ก เขาคิดเลขเก่งและมีความจำเป็นเลิศ ออยเลอร์เข้าเรียนที่มหาวิทยาลัยบาเซิลตอนอายุแค่ 13 ปี อีกเพียง 3 ปีต่อมาเขาก็ได้รับปริญญาโทสาขาปรัชญาซึ่งเป็นเส้นทางไปสู่การเป็นบาทหลวงตามความต้องการของครอบครัว
แต่ระหว่างที่เรียนอยู่เขาใช้เวลาช่วงบ่ายวันเสาร์ไปเรียนคณิตศาสตร์กับอาจารย์ที่มหาวิทยาลัย Johann Bernoulli ผู้เป็นเพื่อนกับพ่อของเขาซึ่งค้นพบความสามารถทางคณิตศาสตร์อันน่าทึ่งของออยเลอร์ Bernoulli จึงไปปรึกษาพ่อของเขาว่าหากออยเลอร์ได้เรียนต่อเขาจะเป็นนักคณิตศาสตร์ผู้ยิ่งใหญ่ของโลกในอนาคต และนั่นทำให้เขาได้กลับไปเรียนคณิตศาสตร์ต่อจนจบปริญญาโทตอนอายุ 19 ปี ออยเลอร์ได้รับปริญญาโท 2 ใบขณะที่เพื่อนวัยเดียวกันเพิ่งจะเข้าเรียนมหาวิทยาลัย
ศาสตราจารย์คณิตศาสตร์และฟิสิกส์

พอเรียนจบออยเลอร์พยายามที่จะเป็นอาจารย์ที่มหาวิทยาลัยบาเซิลแต่ก็ต้องผิดหวังด้วยสาเหตุส่วนหนึ่งเพราะเขาถูกพิจารณาว่ายังเด็กเกินไป ปี 1727 เขาจึงเลือกไปเป็นอาจารย์สอนวิชาฟิสิกส์และคณิตศาสตร์ที่สถาบันวิทยาศาสตร์แห่งรัสเซียที่เมืองเซนต์ปีเตอร์สเบิร์กซึ่ง Daniel Bernoulli เพื่อนของเขา (ลูกของอาจารย์) ไปเป็นอาจารย์สอนคณิตศาสตร์อยู่ก่อนแล้ว ออยเลอร์ประสบความสำเร็จกับการทำงานที่นี่มาก ปี 1730 เขาได้เป็นศาสตราจารย์ฟิสิกส์ และในอีก 3 ปีต่อมาขณะมีอายุ 26 ปีออยเลอร์ได้เป็นศาสตราจารย์คณิตศาสตร์ และยังรับตำแหน่งหัวหน้าแผนกภูมิศาสตร์อีกด้วย
ออยเลอร์ทำงานอยู่ที่เซนต์ปีเตอร์สเบิร์กนาน 14 ปีพร้อมกับสร้างผลงานมากมาย นอกจากงานสอนหนังสือแล้วเขายังเริ่มสร้างผลงานวิจัยและการคิดค้นทางคณิตศาสตร์ในหลายสาขา รวมทั้งฟิสิกส์และวิทยาศาสตร์สาขาอื่น แต่การทำงานในฐานะหัวหน้าแผนกภูมิศาสตร์ของมหาวิทยาลัยกลับสร้างปัญหาด้านสายตาแก่เขาอย่างมาก ออยเลอร์ช่วยทีมนักภูมิศาสตร์ทำแผนที่ของจักรวรรดิรัสเซียทั้งหมด เขาต้องใช้สายตาดูแผนที่จำนวนมากทำให้ดวงตาเขาเริ่มมีปัญหาและต่อมาก็แย่ลงจนทรุดหนักถึงขั้นตาบอดสนิทในอีกหลายปีต่อมา แต่งานดังกล่าวก็เป็นผลงานอีกชิ้นหนึ่งที่เขาภูมิใจ
เจ้าของรางวัล Paris Academy 12 ครั้ง
สถาบัน Paris Academy จัดการแข่งขันตอบปัญหาหรืออธิบายในประเด็นต่างๆด้านคณิตศาสตร์และวิทยาศาสตร์ที่ทางสถาบันตั้งขึ้นมาคล้ายกับหัวข้อวิจัยเพื่อให้นักวิทยาศาสตร์ค้นคว้าวิจัยแล้วส่งผลงานเข้าร่วมแข่งขัน ปี 1727 เป็นปีแรกที่ออยเลอร์ส่งผลงานเข้าร่วมการแข่งขันและเขาได้อันดับที่ 2 แต่ต่อมาเขาชนะการแข่งขันประจำปีรายการนี้ในหัวข้อที่แตกต่างกันถึง 12 ครั้ง อันแสดงถึงความสามารถที่ยอดเยี่ยมในฐานะนักคิดนักวิจัย และมีส่วนให้เขามีชื่อเสียงขจรขจายเป็นที่รู้จักในวงกว้าง
สร้างผลงานค้นคว้าวิจัยที่กรุงเบอร์ลิน

ปี 1741 ด้วยความกังวลกับปัญหาความวุ่นวายทางการเมืองที่เกิดขึ้นในรัสเซียทำให้ออยเลอร์ตัดสินใจรับคำเชิญของพระเจ้าฟรีดริชมหาราชไปเป็นศาสตราจารย์ที่มหาวิทยาลัยเบอร์ลิน เขาทำงานที่นี่นานถึง 25 ปี มีผลงานค้นคว้าวิจัยมากกว่า 380 ชิ้น ครอบคลุมคณิตศาสตร์หลายสาขา รวมถึงวิทยาศาสตร์แขนงอื่น ผลงานหลายชิ้นของเขาเป็นพื้นฐานสำคัญอันนำไปสู่การพัฒนาของคณิตศาสตร์สมัยใหม่ อย่างเช่น ผลงานเรื่อง Introduction to the Analysis of the Infinite ที่ตีพิมพ์ในปี 1748 เป็นพื้นฐานสำคัญของวิชาคณิตวิเคราะห์ (Mathematical Analysis) และผลงานเรื่อง Foundations of Differential Calculus ที่ตีพิมพ์ในปี 1755 ซึ่งเป็นการวางรากฐานของวิชาแคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นต้น
นอกจากนี้ออยเลอร์ยังได้รับมอบหมายให้เป็นครูสอนพิเศษให้แก่หลานสาวของพระเจ้าฟรีดริชมหาราช เขาเขียนจดหมายถึงเธอรวม 234 ฉบับมีเนื้อหาเกี่ยวกับฟิสิกส์และคณิตศาสตร์ ซึ่งต่อมาจดหมายถูกรวมรวมพิมพ์เป็นหนังสือชื่อ Letters to a German Princess, On Different Subjects in Physics and Philosophy และกลายเป็นหนังสือขายดีทั่วยุโรปและอเมริกา หนังสือเล่มนี้แสดงถึงความสามารถในการสื่อสารเรื่องวิทยาศาสตร์กับคนทั่วไปได้อย่างมีประสิทธิภาพซึ่งหาได้ยากสำหรับนักวิจัย และหนังสือเล่มนี้ถูกอ่านอย่างกว้างขวางมากกว่าผลงานด้านคณิตศาสตร์ของเขาเสียอีก
“ไซคลอปส์” ยักษ์ตาเดียวผู้ไม่ย่อท้อ

สายตาของออยเลอร์แย่ลงเรื่อยมาตั้งแต่เริ่มเกิดปัญหาตอนอยู่ที่เซนต์ปีเตอร์สเบิร์ก เมื่อปี 1738 สามปีหลังจากเขาเกือบตายจากการเป็นไข้ ตาข้างขวาก็เกือบจะบอด สายตาของเขาแย่ลงตลอดที่อยู่ในกรุงเบอร์ลิน ปี 1766 เขาเป็นต้อกระจกที่ตาข้างซ้าย หลังจากนั้นไม่นานตาของเขาก็บอดเกือบทั้งหมด แต่การสูญเสียการมองเห็นแทบไม่มีผลต่อการผลิตผลงานของเขาเลย เพราะมันถูกชดเชยด้วยทักษะการคำนวณในใจที่ยอดเยี่ยมและความจำอันเป็นเลิศของเขา
พระเจ้าฟรีดริชมหาราชต้องการสร้างน้ำพุที่พ่นน้ำขึ้นสูง 30 เมตรที่พระราชวัง Sanssouci เมือง Potsdam ซึ่งเป็นเรื่องที่ยากมากในสมัยนั้น และการทำงานก็ล้มเหลวไม่เป็นท่าเนื่องจากท่อส่งน้ำที่ทำด้วยไม้แตกระเบิดเพราะทนแรงดันน้ำอันมหาศาลไม่ไหว ออยเลอร์ถูกขอร้องให้ไปช่วยคำนวณแรงดันน้ำซึ่งเขาพบว่ามันมีค่ามากกว่าที่เคยเข้าใจกัน จึงแนะนำให้ใช้ท่อโลหะแทนท่อไม้และให้ทดลองหารูปร่างและขนาดที่เหมาะสมก่อนสร้างจริง แต่กษัตริย์ไม่ยอมลงทุนมากขนาดนั้นงานสร้างน้ำพุจึงไม่สำเร็จ กษัตริย์ตำหนิออยเลอร์และเรียกเขาว่า “Cyclops” (ยักษ์ตาเดียวในตำนานผู้มีแต่พละกำลังไม่มีสมอง) แต่น้ำพุนี้ถูกสร้างสำเร็จในอีกเกือบร้อยปีต่อมาโดยใช้ท่อเหล็กหล่อกลมขนาดเส้นผ่าศูนย์กลาง 10 นิ้ว
ด้วยความเสียใจและผิดหวังในตัวกษัตริย์ประกอบกับสถานการณ์ทางการเมืองในรัสเซียมีเสถียรภาพดีขึ้นหลังจากที่แคทเธอรีนมหาราชได้ขึ้นครองบัลลังก์ ดังนั้นในปี 1766 ออยเลอร์จึงตอบรับคำเชิญกลับไปทำงานที่มหาวิทยาลัยเซนต์ปีเตอร์สเบิร์กอีกครั้ง แต่มาคราวนี้เขาต้องเจอกับโศกนาฏกรรมหลายอย่าง ปี 1771 ไฟไหม้บ้านเสียหายหมด ตัวเขาเองก็เกือบไม่รอด ปี 1773 เขาต้องสูญเสีย Katharina ภรรยาที่อยู่ด้วยกันมา 40 ปี ออยเลอร์เสียชีวิตแบบกะทันหันด้วยโรคเลือดออกในสมองในปี 1783
ผลงานของนักคณิตศาสตร์อัจฉริยะ

ออยเลอร์มีผลงานการเขียนทางวิชาการมากถึง 30,000 หน้า รวบรวมเป็นหนังสือได้ถึง 75 เล่ม โดยเฉพาะผลงานคณิตศาสตร์มีมากกว่า 900 เรื่อง ครอบคลุมคณิตศาสตร์แทบทุกสาขา ได้แก่ แคลคูลัส, ทฤษฎีกราฟ, โทโปโลยี, ทฤษฎีจำนวนเชิงวิเคราะห์ ฯลฯ เขาเป็นคนแรกที่นำแคลคูลัสเข้าไปประยุกต์ในวิชาฟิสิกส์ และเป็นคนแรกที่ใช้คำว่า “ฟังก์ชัน” ในการบรรยายถึงความสัมพันธ์ที่เกี่ยวข้องกับตัวแปร รวมทั้งยังเป็นผู้คิดค้นสัญลักษณ์สำคัญในทางคณิตศาสตร์อีกหลายอย่างซึ่งยังคงใช้จนถึงปัจจุบัน เรียกได้ว่าใครก็ตามที่เรียนคณิตศาสตร์จะต้องได้พบเจอกับผลงานของออยเลอร์แน่ๆ เพียงแต่จะรู้หรือไม่ว่าสิ่งนั้นเป็นผลงานของเขา ผลงานเด่นของออยเลอร์ที่มักมีการพูดถึงบ่อยๆมีดังต่อไปนี้
Basel Problem – ผลงานการค้นพบสมัยแรกๆในปี 1735 กับการหาคำตอบของอนุกรมอนันต์ของเลขยกกำลังซึ่งยังไม่มีใครทำได้มาเป็นร้อยปี
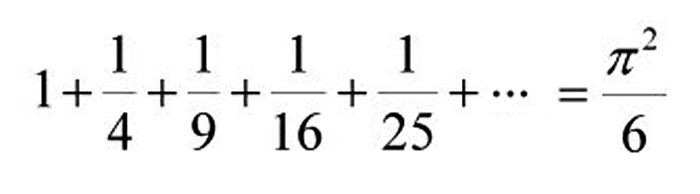
หรือ
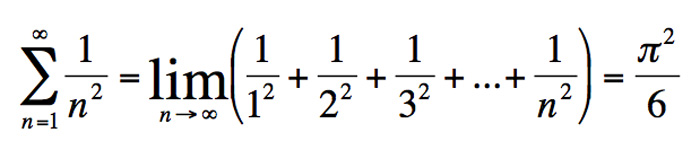
Mechanica – ผลงานที่ตีพิมพ์ในปี 1736 ถือเป็นความก้าวหน้าทางคณิตศาสตร์แบบก้าวกระโดด ออยเลอร์พัฒนาเทคนิคของการวิเคราะห์ทางคณิตศาสตร์และนำไปใช้อธิบายปัญหาการเคลื่อนที่ในวิชากลศาสตร์
Analysis of the Infinite – ผลงานในปี 1748 ที่อาจเรียกได้ว่าเป็นตำราคณิตศาสตร์สมัยใหม่ที่สำคัญที่สุดเล่มหนึ่งในชื่อ Introduction to the Analysis of the Infinite ซึ่งเป็นการศึกษาและวิเคราะห์ฟังก์ชันทางคณิตศาสตร์ผ่านทางอนุกรมอนันต์ซึ่งเป็นสิ่งที่ออยเลอร์เชี่ยวชาญเป็นพิเศษ
Differential Calculus – ออยเลอร์วางรากฐานของวิชาแคลคูลัสเชิงอนุพันธ์ซึ่งมีประโยชน์อย่างยิ่งต่อการประยุกต์ใช้กับวิชาฟิสิกส์ไว้ในผลงานชื่อ Foundations of Differential Calculus ซึ่งตีพิมพ์ในปี 1755
Language of Mathematics – ออยเลอร์ริเริ่มการใช้สัญลักษณ์ทางคณิตศาสตร์มากมายซึ่งเป็นที่นิยมและยังใช้งานจนถึงปัจจุบัน
- ใช้ f(x) แทนฟังก์ชันของ x
- ใช้ i แทนหน่วยจินตภาพ (
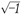 )
) - ใช้ π แทนค่า pi
- ใช้ e แทนค่าคงตัวออยเลอร์ซึ่งมีค่าเท่ากับ 2.718281…
- ใช้ Σ แทนผลรวมใดๆ
- ใช้ x, y, z แทนตัวแปรหรือตัวไม่ทราบค่า (Unknown) ในสมการ
Euler’s formula – สูตรคณิตศาสตร์ในสาขาการวิเคราะห์เชิงซ้อนที่แสดงความสัมพันธ์ระหว่างฟังก์ชันตรีโกณมิติกับฟังก์ชันเลขชี้กำลังเชิงซ้อน ออยเลอร์คิดค้นสูตรนี้ราวปี 1748 และมันถูกเรียกว่าเป็นสูตรที่โดดเด่นที่สุดในคณิตศาสตร์
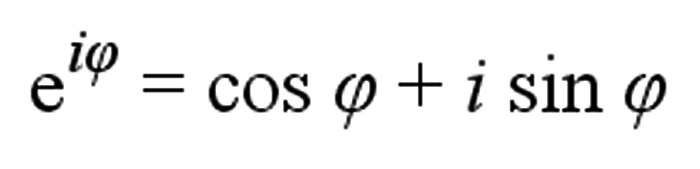
และเมื่อแทนค่ามุม ω ด้วยค่า π ในสูตรของออยเลอร์จะได้เป็น
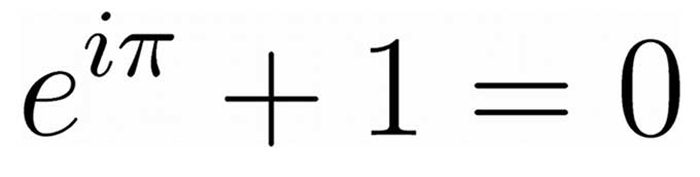
เรียกว่าเอกลักษณ์ของออยเลอร์ (Euler’s identity) ซึ่งเป็นกรณีพิเศษของสูตรออยเลอร์ (Euler’s formula) เป็นสูตรคณิตศาสตร์ที่โดดเด่นมากเนื่องจากใช้ทั้งเครื่องหมายบวก คูณ ยกกำลัง และเท่ากับเพียงครั้งเดียว และยังใช้ค่าคงที่สำคัญถึง 5 ตัวคือ 0, 1, e, i และ π ได้รับการโหวตให้เป็น “สูตรคณิตศาสตร์ที่งดงามที่สุดเท่าที่เคยมีมา” เมื่อปี 1988
Euler’s Polyhedral Formula – สูตรคณิตศาสตร์ในสาขาโทโปโลยีใช้กับรูปทรงหลายหน้าสามมิติ (Polyhedron) แสดงความสัมพันธ์ระหว่างจำนวนจุดยอด (V), จำนวนขอบ (E) และจำนวนหน้า (F) ได้อย่างน่าทึ่ง และสามารถใช้กับรูปทรงหลายหน้านูนทั้งหมด
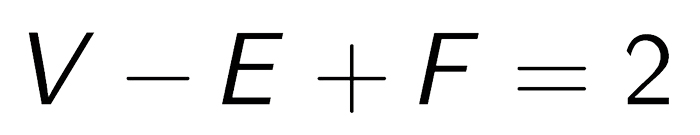
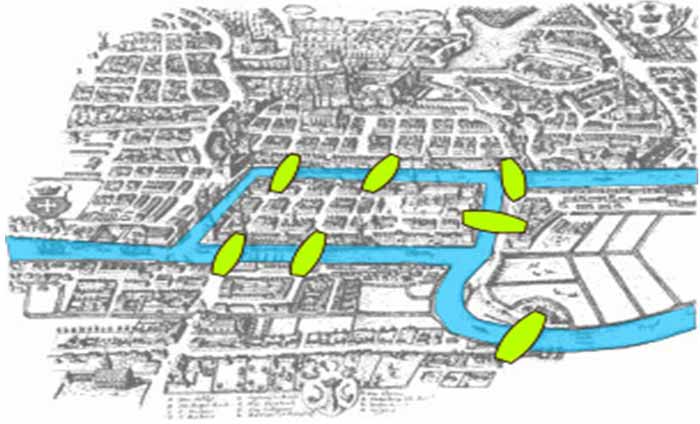
Seven Bridges of Königsberg – ออยเลอร์แสดงการแก้ปัญหาเรื่องสะพานทั้งเจ็ดแห่งเมืองเคอนิชส์แบร์คที่มีผู้ตั้งคำถามว่าเป็นไปได้หรือไม่ที่สามารถข้ามสะพานทั้ง 7 แห่งเพียงครั้งเดียวและกลับมายังจุดเริ่มต้นได้ การพิสูจน์ของเขาว่าเป็นไปไม่ได้นั้นกลายเป็นทฤษฎีบทแรกของทฤษฎีกราฟ
ชื่อออยเลอร์ถูกนำไปตั้งเป็นชื่อของสูตร, สมการ, ฟังชั่น, ระเบียบวิธี, ค่าคงตัว ฯลฯ เพื่อใช้ทั้งในคณิตศาสตร์และวิทยาศาสตร์จำนวนกว่า 30 รายการ และดูเหมือนออยเลอร์จะเป็นคนเดียวที่ชื่อถูกนำไปใช้เป็นชื่อค่าคงตัว 2 อย่างคือ e (Euler’s number) = 2.718281… และ γ (Euler’s constant) = 0.577215… ด้วยผลงานสำคัญจำนวนมากมายเหลือคณานับของเขาที่ครอบคลุมคณิตศาสตร์แทบทุกสาขาทำให้ออยเลอร์ได้รับการยกย่องเป็นนักคณิตศาสตร์อัจฉริยะผู้ยิ่งใหญ่ที่มีผลงานมากที่สุดในโลก

ข้อมูลและภาพจาก famousscientists, revolvy, wikipedia



