เด็กอัจฉริยะกำเนิดในครอบครัวยากจน

เกาส์เป็นชาวเยอรมันเกิดเมื่อปี 1777 ที่เมืองเบราน์ชไวค์ (Brunswick) ประเทศเยอรมันในครอบครัวยากจน แม่ของเกาส์เป็นคนฉลาดแต่ไม่รู้หนังสือ เป็นแม่บ้าน ส่วนพ่อทำงานรับจ้างใช้แรงงาน ครอบครัวของเกาส์ไม่เคยมีเงินพอใช้ แต่เกาส์เป็นเด็กอัจฉริยะคิดเลขเป็นก่อนพูดได้ ตอนสามขวบเคยบอกพ่อให้แก้ไขการคำนวณค่าจ้างคนงานที่พ่อคิดผิด ตอนอายุ 7 ปีเกาส์สร้างความประหลาดใจให้แก่คุณครูที่โรงเรียนเมื่อเขาใช้เวลาไม่กี่วินาทีตอบโจทย์การบวกเลขตั้งแต่ 1 ถึง 100 ในห้องเรียนจนคุณครูตะลึง ยิ่งเมื่อทราบวิธีคิดยิ่งทึ่งมากขึ้นไปอีก
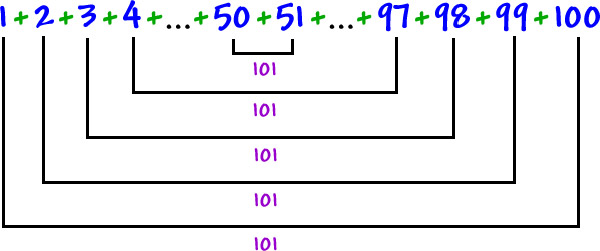
สำหรับเด็กชั้นประถมการบวกเลขตั้งแต่ 1 ถึง 100 ถือเป็นโจทย์ที่ยากมากและใช้เวลานานมากจนไม่อยากทำ แต่เกาส์บอกคุณครูว่าเขาใช้วิธีจับคู่ตัวแรกสุดคือ 1 กับตัวสุดท้ายคือ 100 บวกกันได้ 101 คู่ถัดไปเป็น 2 กับ 99 บวกกันได้ 101 เช่นกัน จับคู่ไปแบบนี้จนครบจะได้ทั้งหมด 50 คู่ คำตอบจึงเท่ากับ 101 บวกกัน 50 ตัว หรือเท่ากับ 101 x 50 = 5050 ซึ่งใช้เวลาคิดเพียงไม่กี่วินาที
ความอัจฉริยะของเกาส์ทำให้คุณครูมองเห็นว่าเขาอาจจะเป็นศาสตราจารย์คณิตศาสตร์ผู้ยิ่งใหญ่ในอนาคต แต่อุปสรรคสำคัญคือความยากจนของครอบครัว คุณครูจึงช่วยพูดคุยให้พ่อของเกาส์ส่งเสริมเรื่องการเรียนอย่าเพิ่งให้เขาออกไปทำงานหาเงินช่วยครอบครัว จนเมื่อเกาส์อายุได้ 10 ปีเขาสามารถพิสูจน์ทฤษฎีบททวินาม (Binomial Theorem) ได้เอง เรื่องความอัจฉริยะของเกาส์จึงไปเข้าหูของดยุกแห่งเบราน์ชไวค์ผู้ซึ่งได้เข้ามาให้การสนับสนุนค่าใช้จ่ายในการเรียนของเขาอย่างเต็มที่ ปี 1792 ตอนอายุ 15 ปีเกาส์ได้เข้าเรียนที่วิทยาลัย Caroline College และสำเร็จการศึกษาด้านคณิตศาสตร์เมื่อมีอายุ 18 ปี
นักศึกษาผู้มีผลงานยิ่งกว่าศาสตราจารย์
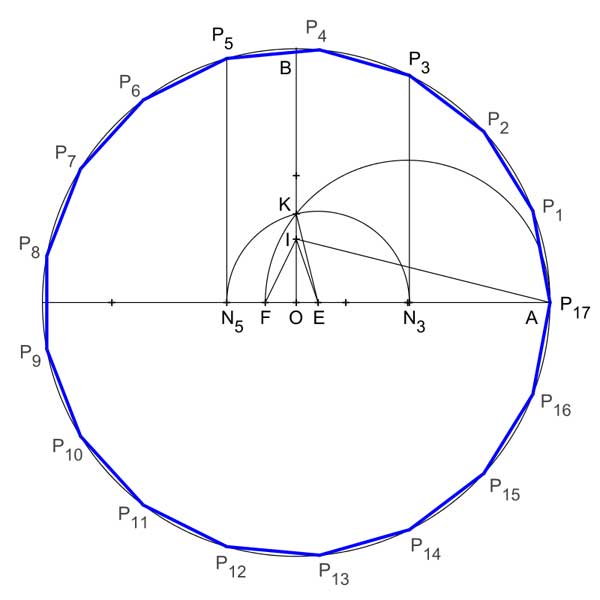
เกาส์เข้าเรียนต่อระดับปริญญาเอกที่มหาวิทยาลัยเกิททิงเงิน (University of Göttingen) ในปี 1795 เพียงแค่ 6 เดือนแรกในรั้วมหาวิทยาลัยเขาก็สามารถแก้ปัญหาโจทย์ที่นักคณิตศาสตร์คิดไม่ออกมานาน 2,000 ปีได้สำเร็จนั่นคือการสร้างรูป 17 เหลี่ยมด้านเท่าด้วยไม้บรรทัดและวงเวียน ชาวกรีกโบราณค้นพบวิธีสร้างรูป 3, 5, และ 15 เหลี่ยมด้านเท่าได้โดยใช้แค่ไม้บรรทัดและวงเวียน แต่หลังจากนั้นไม่มีใครสามารถคิดวิธีสร้างรูปหลายเหลี่ยมด้านเท่าที่มีจำนวนด้านเป็นเลขคี่เพิ่มได้อีกเลยจนกระทั่งเกาส์คิดได้สำเร็จ และที่ยิ่งไปกว่านั้นเขายังค้นพบสูตรคณิตศาสตร์ที่สามารถหารูปหลายเหลี่ยมด้านเท่าทั้งหมดที่สามารถสร้างขึ้นได้ด้วยการใช้แค่ไม้บรรทัดและวงเวียน และกรณีจำนวนด้านเป็นเลขคี่สามารถทำได้เพียง 31 รูปคือรูป 3, 5, 15,17, 51, 85, 255, 257, …. , และ 4,294,967,295 เหลี่ยม เกาส์ภูมิใจกับผลงานเรื่องนี้มากขนาดขอให้สลักรูป 17 เหลี่ยมด้านเท่าไว้บนแผ่นหินจารึกหน้าหลุมฝังศพของเขาด้วย
ระหว่างที่เป็นนักศึกษาเกาส์ได้คิดค้นความรู้ใหม่ทางคณิตศาสตร์มากมายหลายอย่างซึ่งนำความเปลี่ยนแปลงและความก้าวหน้าทางคณิตศาสตร์อย่างมาก หลังจากเขาค้นพบเรื่อง 17 เหลี่ยมด้านเท่าได้ไม่นานเขาได้เสนอระบบเลขคณิตมอดุลาร์ (Modular arithmetic) ตามมาด้วยการเป็นคนแรกที่พิสูจน์การแลกเปลี่ยนกำลังสอง (Quadratic reciprocity) และการค้นพบใหม่อีกหลายเรื่อง ในวิทยานิพนธ์ปริญญาเอกเกาส์ได้เสนอเรื่องทฤษฎีบทมูลฐานของพีชคณิต (Fundamental Theorem of Algebra) และเขาเป็นคนแรกที่พิสูจน์ได้ว่าทุกสมการพหุนามอันดับใดๆจะมีคำตอบอยู่ในรูปจำนวนเชิงซ้อนเสมอ ทฤษฎีบทนี้นักคณิตศาสตร์ชื่อดังในอดีตหลายคนได้เคยพยายามพิสูจน์แล้วแต่มาสำเร็จด้วยฝีมือของเกาส์ และไม่เพียงเท่านี้ตลอดช่วงชีวิตของเกาส์เขาได้พิสูจน์ทฤษฎีบทนี้ถึง 4 รูปแบบที่ต่างกันโดยสิ้นเชิง
ปี 1798 ขณะที่เกาส์มีอายุ 21 ปี ปีเดียวกับที่เขาเรียนจบปริญญาเอกเกาส์ได้รวบรวมผลงานของเขาเกี่ยวกับทฤษฎีจำนวนเขียนหนังสือ Disquisitiones Arithmeticae ในภาษาลาตินซึ่งได้รับการตีพิมพ์ครั้งแรกในปี 1801 และกลายเป็นตำราทฤษฎีจำนวนที่สำคัญที่สุดในประวัติศาสตร์ ความสำคัญของหนังสือเล่มนี้ต่อทฤษฎีจำนวนเทียบได้กับความสำคัญของหนังสือ Elements ของ Euclid ที่มีต่อเรขาคณิต ผลงานด้านคณิตศาสตร์ที่ยอดเยี่ยมของเกาส์จำนวนมากเหล่านี้เกิดขึ้นในขณะที่เขายังเป็นนักศึกษาเท่านั้นซึ่งยิ่งตอกย้ำความเป็นอัจฉริยะด้านคณิตศาสตร์ของเกาส์ชนิดที่หาใครเทียบได้ยาก

ยอดนักคณิตศาสตร์ที่เชี่ยวชาญทุกสาขา

หลังจากการค้นพบวิธีสร้างรูป 17 เหลี่ยมด้านเท่าเกาส์ก็แน่ใจว่าเขาจะเป็นนักคณิตศาสตร์ระดับแนวหน้าคนหนึ่งในประวัติศาสตร์ เขาได้เริ่มบันทึกสิ่งที่เขาค้นพบลงในสมุดไดอารี่ แน่นอนว่าเรื่องแรกคือเรื่อง 17 เหลี่ยมด้านเท่า เกาส์บันทึกความรู้ใหม่ทางคณิตศาสตร์ที่เขาค้นพบตั้งแต่ปี 1796 ถึงปี 1814 รวมทั้งสิ้น 146 เรื่อง ปี 1796 เป็นปีที่มหัศจรรย์มากเพราะมีบันทึกถึง 49 เรื่อง ในบันทึกเรื่องที่ 18 เขาค้นพบว่าจำนวนเต็มทุกจำนวนสามารถเขียนในรูปผลบวกของจำนวนสามเหลี่ยม (Triangular number) 3 ตัว โดยเขาบันทึกไว้อย่างน่าสนใจว่า
Ε Υ Ρ Η Κ Α! num = Δ + Δ + Δ
คำ Ε Υ Ρ Η Κ Α เป็นภาษากรีกโบราณหมายถึง Eureka เกาส์ใช้คำนี้แสดงการค้นพบเลียนแบบอาร์คิมิดีสผู้เป็นฮีโร่คนสำคัญของเขานั่นเอง สมุดไดอารี่เล่มนี้สูญหายไปหลังจากเกาส์เสียชีวิตนานกว่า 40 ปีมาถูกค้นพบอีกครั้งในปี 1897 และตีพิมพ์เผยแพร่ในปี 1903
ผลงานด้านคณิตศาสตร์ของเกาส์มีจำนวนมากและหลากหลายกว้างขวางครอบคุมเกือบทุกสาขาของคณิตศาสตร์ ไม่ว่าเขาจับเรื่องใดก็จะพบความรู้ที่สำคัญและพบวิธีคำนวณใหม่ซึ่งเป็นรากฐานของวิชานั้นอยู่เสมอ และต่อไปนี้เป็นผลงานสำคัญบางส่วนของเขาในหลากหลายสาขาของคณิตศาสตร์
ทฤษฎีจำนวน – ผลงานด้านทฤษฎีจำนวนของเกาส์มีมากมายหลายเรื่องและถือว่าโดดเด่นที่สุด หนังสือ Disquisitiones Arithmeticae ของเขาเป็นจุดเริ่มต้นและเป็นพื้นฐานสำคัญตลอดจนกำหนดรูปแบบของทฤษฎีจำนวนสมัยใหม่มาจนถึงปัจจุบัน นอกจากนี้เกาส์ได้ริเริ่มการใช้สัญลักษณ์ ‘≡‘หรือความเท่ากันทุกประการไว้ในหนังสือเล่มนี้ด้วย บางคนยกย่องเขาเป็นบิดาแห่งทฤษฎีจำนวน
พีชคณิต – ผลงานการพิสูจน์ทฤษฎีบทมูลฐานของพีชคณิต (Fundamental Theorem of Algebra) ในวิทยานิพนธ์ปริญญาเอก รวมทั้งการพิสูจน์ทฤษฏีบทนี้ด้วยวิธีการที่แตกต่างกันอีก 3 รูปแบบในเวลาต่อมายืนยันถึงเชี่ยวชาญของเกาส์ นอกเหนือจากผลงานด้านพีชคณิตอื่นๆอีกจำนวนมาก
เรขาคณิต – การที่เกาส์ค้นพบวิธีสร้างรูป 17 เหลี่ยมด้านเท่าด้วยไม้บรรทัดและวงเวียนไม่ได้เป็นเพียงการแก้ปัญหาเรขาคณิตขั้นสูงเท่านั้น แต่เขายังได้แสดงวิธีพิสูจน์เรื่องนี้โดยใช้วิธีถอดสมการ x16 + x15 + x14 ….+ 1 = 0 ซึ่งเป็นเทคนิคใหม่ที่ทำให้โลกรู้วิธีแก้ปัญหาเรขาคณิตโดยวิธีพีชคณิต นอกจากนี้เกาส์ยังมีผลงานในเรื่องเรขาคณิตเชิงอนุพันธ์ซึ่งเกี่ยวข้องกับเส้นโค้งและพื้นผิวจนเป็นที่รู้จักในชื่อ Gaussian curvature รวมทั้งเขายังเป็นคนแรกๆที่ศึกษาและพัฒนาเรขาคณิตนอกระบบยูคลิด (non-Euclidean geometry) เพียงแต่ไม่ได้ตีพิมพ์ออกเผยแพร่
จำนวนเชิงซ้อน – จำนวนเชิงซ้อนเป็นที่รู้จักในหมู่นักคณิตศาสตร์มาตั้งแต่สมัยเรอเนสซองส์แต่ไม่ค่อยมีคนสนใจนำมาใช้ประโยชน์ จนกระทั่งเกาส์ได้เสนอแทนจำนวนเชิงซ้อนด้วยจุดในระนาบของกราฟที่มีแกนแนวนอนเป็นจำนวนจริงและแกนแนวตั้งเป็นจำนวนจินตภาพ และให้แทน a + bi ด้วยคู่อันดับ (a, b) และขยายคุณสมบัติต่างๆของจำนวนเชิงซ้อนจนต่อมาเป็นที่ยอมรับกันทั่วโลก นอกจากนี้เขายังใช้จำนวนเชิงซ้อนในการพิสูจน์ทฤษฎีบทมูลฐานของพีชคณิตอีกด้วย
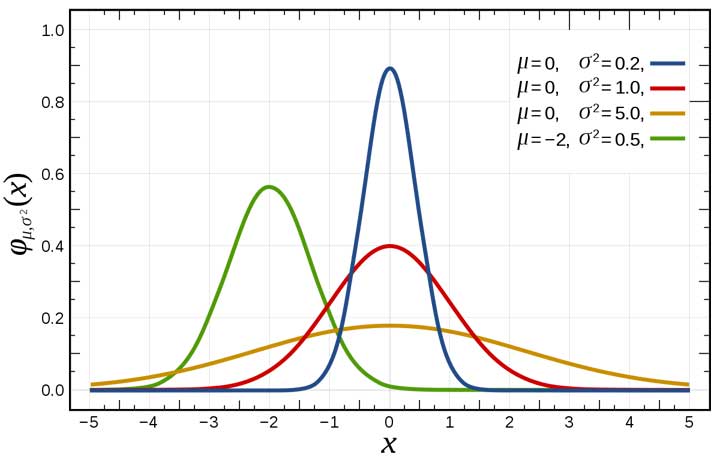
สถิติและความน่าจะเป็น – เกาส์เป็นผู้คนพบวิธีกำลังสองน้อยที่สุด (Least Squares Method) และการกระจายตัวแบบปกติ (Normal Distribution) หรือกราฟเส้นโค้งรูประฆังคว่ำที่มักเรียกกันว่าการกระจายตัวแบบเกาส์ (Gaussian Distribution) อันเป็นหัวใจและพื้นฐานสำคัญของวิชาสถิติศาสตร์ (Statistics) และวิชาความน่าจะเป็น (Probability)
นักคณิตศาสตร์รุ่นหลังต่างก็ยอมรับว่ามีผลงานของเกาส์อยู่ทุกที่ในวิชาคณิตศาสตร์ เขาได้รับการยกย่องว่าเป็นนักคณิตศาสตร์ที่ยิ่งใหญ่ที่สุดนับจากยุคโบราณ และเป็นนักคณิตศาสตร์ที่เชี่ยวชาญรอบรู้ทุกเรื่องคนสุดท้ายของโลกซึ่งก็น่าจะจริงเพราะในปัจจุบันคณิตศาสตร์ได้พัฒนากว้างขวางแยกย่อยและลึกซึ้งอย่างมากสุดที่มนุษย์คนหนึ่งจะเรียนรู้จนเชี่ยวชาญได้หมดแม้ว่าจะมีความอัจริยะเช่นเดียวกับเกาส์ก็ตาม
คณิตศาสตร์นำทางให้เป็นนักดาราศาสตร์

เมื่อปี 1766 Johann Daniel Titius พบว่าระยะห่างจากดวงอาทิตย์ของดาวเคราะห์สอดคล้องกับอนุกรมของเลขจำนวนเต็มคือ 4, 7, 10, 16, 28, 52, 100, 196 (อนุกรม a = 2n x 3 + 4 เมื่อ n = -∞, 0,1, 2, 3, …) โดยตอนที่ Titius เสนอเรื่องนี้มีการค้นพบดาวพุธ ดาวศุกร์ โลก ดาวอังคาร ดาวพฤหัสบดี และดาวเสาร์แล้วและมีระยะห่างจากดวงอาทิตย์ใกล้เคียงกับตัวเลข 4, 7, 10, 16, 52, 100 หน่วย (ตัวเลขเหล่านี้หารด้วย 10 จะมีหน่วยเป็น AU หรือระยะทางจากโลกถึงดวงอาทิตย์) แต่ยังไม่มีการค้นพบดาวเคราะห์ที่ระยะ 28 และ 196 จนถึงปี 1781 William Herschel ค้นพบดาวยูเรนัสที่ระยะ 196 หน่วยตรงกับคำทำนายของ Titius พอดี นักดาราศาสตร์ทั่วโลกจึงหันมาสนใจค้นหาดาวเคราะห์ที่อยู่ห่างจากดวงอาทิตย์ที่ระยะ 28 หน่วย
ไม่น่าเชื่อว่าในปี 1801 Giuseppe Piazzi ได้ค้นพบดาวเคราะห์ซึ่งอยู่ที่ระยะห่าง 28 หน่วยซึ่งก็คือดาว Ceres แต่ด้วยขนาดที่เล็กมากมันจึงถูกเรียกเป็นดาวเคราะห์น้อย (ปัจจุบันเรียกว่าดาวเคราะห์แคระ) Piazzi ติดตามดาว Ceres ได้เพียง 6 สัปดาห์เขาเกิดป่วยหนักพอหายกลับมาก็หา Ceres ไม่เจอแล้ว ข้อมูลที่เขาติดตามมันมีเพียงราว 3 องศาเท่านั้นไม่สามารถใช้คำนวณวงโคจรได้ และก็ไม่มีนักดาราศาสตร์คนไหนหามันพบ เกาส์สนใจเรื่องนี้เขาคำนวณหาตำแหน่งและวงโคจรดาว Ceres จากข้อมูลที่มีเพียงน้อยนิดได้สำเร็จด้วยการคิดค้นเทคนิค Least Squares Method และ Normal Distribution เข้ามาแก้ปัญหา หลังจากที่เขาเสนอผลการทำนายตำแหน่งของ Ceres ได้ไม่ถึงเดือนก็มีนักดาราศาสตร์ใช้ตำแหน่งที่เขาระบุค้นหามันจนพบ โดยตำแหน่งจริงคลาดเคลื่อนจากที่เกาส์ทำนายเพียงแค่ครึ่งองศา
ความสำเร็จในเรื่องนี้ทำให้เกาส์ได้รับตำแหน่งศาสตราจารย์ดาราศาสตร์และเป็นผู้อำนวยการคนแรกของหอดูดาวของมหาวิทยาลัยเกิททิงเงินซึ่งเริ่มสร้างในปี 1803 เสร็จในปี 1816 ในฐานะนักดาราศาสตร์เกาส์ได้ศึกษาการเคลื่อนที่ของดาวเคราะห์น้อยซึ่งได้รับอิทธิพลจากดาวเคราะห์ขนาดใหญ่และได้ตีพิมพ์ทฤษฎีการเคลื่อนที่ของวัตถุท้องฟ้า Theory of Motion of the Celestial Bodies โดยเขาได้ปรับปรุงวิธีทางคณิตศาสตร์ที่ใช้ในการคำนวณวงโคจร มีการนำเอาเทคนิค Least Squares Method เข้ามาประยุกต์ใช้ด้วย ซึ่งได้กลายเป็นรากฐานสำคัญของการคำนวณทางดาราศาสตร์ เกาส์ทำงานในตำแหน่งนี้จนตลอดชีวิต
นักฟิสิกส์ผู้โดดเด่นด้านไฟฟ้าและแม่เหล็ก

เกาส์มิได้นำเอาความเชี่ยวชาญด้านคณิตศาสตร์ไปประยุกต์ใช้เพียงในงานด้านดารศาสตร์เท่านั้น เขายังนำไปประยุกต์ใช้กับงานรังวัดบนสัณฐานโลก (Geodetic Survey) ที่ต้องคำนึงถึงความโค้งของผิวโลกด้วย ราวปี 1821เกาส์ได้รับการแต่งตั้งเป็นที่ปรึกษาในโครงการสำรวจอาณาจักรฮันโนเวอร์ ซึ่งนอกจากเกาส์ได้พัฒนาทฤษฎีทางคณิตศาสตร์เกี่ยวกับเส้นโค้งและพื้นผิวโค้งเพื่อใช้ในงานนี้แล้ว เขายังได้ประดิษฐ์อุปกรณ์สำรวจ Heliotrope ที่ใช้กระจกสะท้อนแสงอาทิตย์ระยะไกลมากมาช่วยเพิ่มความแม่นยำในงานสำรวจอีกด้วย
ตั้งแต่ปี 1831 เกาส์ได้ร่วมกับ Wilhelm Weber นักฟิสิกส์รุ่นน้องอายุน้อยกว่าเขา 27 ปีทำการศึกษาวิจัยเกี่ยวกับสนามแม่เหล็กโลกจนกระทั่งได้ความรู้ใหม่เกี่ยวกับแม่เหล็กมากมาย รวมทั้งการคิดค้นหน่วยสนามแม่เหล็กในรูปแบบของมวล, ประจุ และเวลา และยังทำวิจัยต่อเนื่องจนค้นพบกฎเกี่ยวกับการกระจายแรงดันและกระแสไฟฟ้าซึ่งต่อมามีการพัฒนาเป็น Kirchhoff’s circuit laws หลังจากนั้นเกาส์ได้ใช้ความสามารถด้านคณิตศาสตร์อันเอกอุของเขาวิเคราะห์พฤติกรรมของสนามไฟฟ้าและสนามแม่เหล็กพัฒนาเป็น Gauss’s law ที่ประกอบด้วยสมการสำคัญ 2 สมการคือ
กฎของเกาส์ทั้ง 2 สมการนี้เป็นส่วนประกอบใน 4 สมการสำคัญที่ทำให้สามารถรวมสนามแม่เหล็กและสนามไฟฟ้าให้กลายเป็นสิ่งเดียวคือสนามแม่เหล็กไฟฟ้าที่ James Clerk Maxwell เป็นผู้ทำสำเร็จ นอกจากนี้เกาส์กับ Weber ยังได้คิดค้นและติดตั้งระบบโทรเลขขึ้นเป็นครั้งแรกใช้ติดต่อสื่อสารระหว่างหอดูดาวของเกาส์และตึกฟิสิกส์ของ Weber ที่อยู่ห่างกันราว 2.5 กิโลเมตร นักวิทยาศาสตร์รุ่นหลังให้การยกย่องในความสามารถและผลงานอันยอดเยี่ยมในด้านไฟฟ้าและแม่เหล็กโดยการใช้ชื่อของเขาเป็นชื่อหน่วยของความหนาแน่นฟลักซ์แม่เหล็กหรือการเหนี่ยวนำแม่เหล็กคือหน่วย Gauss (G)
ศาสตราจารย์ผู้ไม่ชอบสอนและการโต้แย้ง

แม้ว่าเกาส์จะเป็นอาจารย์มหาวิทยาลัยแต่เขาไม่ค่อยชอบสอนหนังสือ และตอนที่เขาบรรยายเขาต้องการให้นักศึกษาตั้งใจฟังเขามากกว่าจดเลคเชอร์ เรื่องที่เขาสอนมักจะเป็นความรู้ขั้นพื้นฐานที่ไม่ค่อยเชื่อมโยงกับงานที่เขาทำวิจัยซึ่งเป็นความรู้ในเชิงลึก สาเหตุหนึ่งที่ทำให้เขารับตำแหน่งผู้อำนวยการหอดูดาวก็เพราะว่าตำแหน่งนี้มีชั่วโมงเลคเชอร์น้อยนั่นเอง ถึงกระนั้นก็ตามเกาส์ก็ยังมีลูกศิษย์เก่งๆหลายคนที่เป็นนักคณิตศาสตร์ชั้นแนวหน้าของโลก เช่น Bernhard Riemann และ Richard Dedekind เป็นต้น
ผลงานที่ตีพิมพ์ของเกาส์แต่ละอย่างนั้นส่งผลกระทบต่อวงการวิชาการอย่างมหาศาล แต่ยังมีผลงานของเกาส์ที่ไม่ได้ตีพิมพ์อีกจำนวนมากซึ่งมีความสำคัญยิ่งใหญ่ไม่แพ้กัน เช่น ในปี 1820 เกาส์ค้นพบเรขาคณิตนอกระบบยูคลิด (non-Euclidean geometry) ซึ่งมีความสำคัญต่อจินตนาการของมนุษย์ที่มีต่อธรรมชาติและโครงสร้างจักรวาล เทียบเคียงได้กับการปฏิวัติของโคเปอร์นิคัสในสาขาดาราศาสตร์เลยทีเดียว แต่เขาไม่ได้เปิดเผยผลงานชิ้นนี้ต่อสาธารณะ จนกระทั่่งถึงปี 1832 Johann Bolyai ได้ตีพิมพ์เรื่องเดียวกันนี้ พอพ่อของ Bolyai ที่เป็นเพื่อนกับเกาส์นำข่าวมาบอกเขาก็ไปรื้อผลงานเก่าในลังออกมาให้ดู Bolyai ผู้ลูกถึงกับพูดว่า “ผมรู้สึกเหมือนเดินอยู่ในฝ่ามือของยักษ์ใหญ่”
สาเหตุที่เกาส์ไม่ยอมตีพิมพ์ผลงานบางชิ้นเป็นเพราะเขามีนิสัยรักสันโดษและความสงบไม่ชอบการโต้แย้ง อย่างเรื่องเรขาคณิตนอกระบบยูคลิดถ้าหากเขาตีพิมพ์ออกไปก็จะต้องไปขัดแย้งกับความเชื่อเก่าที่ฝังลึกอยู่กับระบบเรขาคณิตของยุคลิดมาช้านาน เขาคิดว่าการโต้แย้งกับคนโง่คือการเสียเวลา อีกอย่างหนึ่งเกาส์ต้องการผลงานที่สมบูรณ์แบบที่มิอาจโต้แย้งได้ หากผลงานชิ้นไหนเขาเห็นว่ายังมีช่องว่างที่อาจผิดพลาดหรือถูกโต้แย้งได้เขาก็จะไม่ตีพิมพ์งานชิ้นนั้น ลักษณะเช่นนี้มีส่วนคล้ายกับไอแซก นิวตันที่มีผลงานสำคัญซึ่งไม่ได้ตีพิมพ์อยู่จำนวนมากเช่นกัน
อัจฉริยะตัวจริงฉายาเจ้าชายคณิตศาสตร์

เกาส์ (Gauss) ผู้เสียชีวิตด้วยโรคเกาต์ (Gout) ในปี 1855 เป็นหนึ่งในสุดยอดนักคณิตศาสตร์ผู้ยิ่งใหญ่ที่สุดตลอดกาล 4 คนที่ประกอบด้วยเกาส์, เลออนฮาร์ด ออยเลอร์, ไอแซก นิวตัน และอาร์คิมิดีส ด้วยความเป็นอัจฉริยะตัวจริงด้านคณิตศาสตร์และผลงานที่ยิ่งใหญ่หลากหลายแทรกซึมในทุกสาขาของคณิตศาสตร์เขาจึงได้รับฉายาว่า “เจ้าชายแห่งคณิตศาสตร์” (Prince of Mathematics) และเกาส์ยังมีผลงานที่โดดเด่นด้านดาราศาสตร์และฟิสิกส์ โดยเฉพาะอย่างยิ่งทางด้านไฟฟ้าและแม่เหล็ก ดังนั้นหากจะบอกว่า ‘ไอแซก นิวตัน’ คือสุดยอดนักฟิสิกส์ที่เก่งคณิตศาสตร์มากที่สุด ในทางกลับกัน ‘เกาส์’ ก็คือสุดยอดนักคณิตศาสตร์ที่เก่งฟิสิกส์มากที่สุด
ข้อมูลและภาพจาก famousscientists.org, wikipedia, britannica