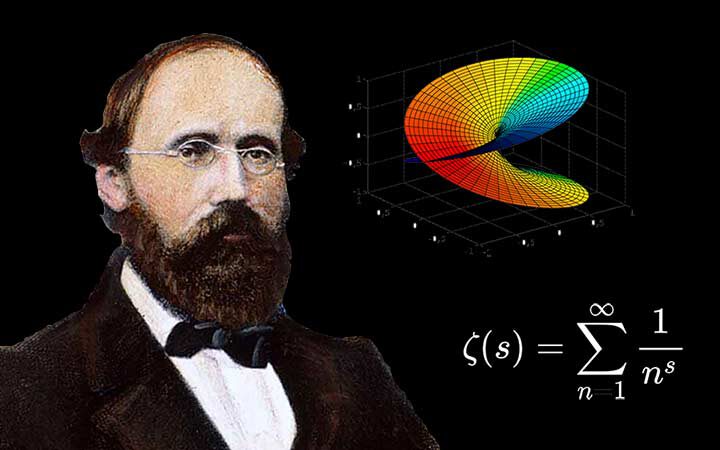แบร์นฮาร์ด รีมันน์ เป็นชาวเยอรมัน เกิดเมื่อปี 1826 ที่หมู่บ้าน Breselenz ในเมือง Dannenberg ทางตอนเหนือของเยอรมัน เป็นลูกคนที่สองจากทั้งหมดหกคนของบาทหลวงจนๆคนหนึ่งในเมือง ส่วนแม่ก็เสียชีวิตไปก่อนที่พวกลูกๆจะโตเป็นผู้ใหญ่ ในวัยเด็กรีมันน์และพี่น้องมีชีวิตอยู่แบบยากจนและถูกคุกคามจากวัณโรค พี่น้องของเขาหลายคนเสียชีวิตไปขณะอายุยังน้อย ตัวรีมันน์เองสุขภาพไม่ค่อยจะดีนักแถมยังเป็นคนขี้อายพูดไม่ค่อยเป็นแต่เริ่มฉายแววความเก่งกาจทางด้านคณิตศาสตร์ออกมาให้เห็น พ่อจึงหาครูแถวบ้านมาสอนคณิตศาสตร์ให้กับลูกชายวัย 10 ปีของเขา แต่เพียงไม่นานเขาก็พบว่าลูกชายเก่งกว่าครูเสียแล้ว
ปี 1840 รีมันน์ถูกส่งไปเรียนชั้นมัธยมที่เมือง Hanover ซึ่งอยู่ไกลจากบ้านมากเขาต้องไปอาศัยอยู่กับยาย สองปีต่อมายายเสียชีวิตเขาจึงย้ายไปเรียนที่เมือง Lüneburg ช่วงที่เรียนชั้นมัธยมรีมันน์ได้เรียนภาษาละติน กรีก ฮีบรู และเยอรมัน รวมทั้งศึกษาพระคัมภีร์อย่างเข้มข้นเพื่อเตรียมตัวเป็นบาทหลวงตามรอยของพ่อ แต่เขายังคงหลงใหลกับวิชาคณิตศาสตร์และความสามารถในการแก้ปัญหาคณิตศาสตร์ที่ซับซ้อนอย่างเชี่ยวชาญมักสร้างความประหลาดใจให้กับครูของเขาอยู่เสมอ ครูคนหนึ่งเคยให้เขายืมหนังสือคณิตศาสตร์ระดับสูงไปอ่านหลายเล่ม รวมทั้งหนังสือของ Leonhard Euler และ Adrien-Marie Legendre ปรากฏว่ารีมันน์ใช้เวลาแค่เพียงสัปดาห์เดียวก็สามารถอ่านทำความเข้าใจได้หมดทั้งเล่ม ทั้งๆที่แม้แต่นักศึกษาระดับมหาวิทยาลัยยังต้องใช้เวลาศึกษานานนับเดือนกว่าจะเข้าใจ
ลูกศิษย์ของเจ้าชายแห่งคณิตศาสตร์

ปี 1846 พ่อของรีมันน์ส่งเขาไปเรียนที่มหาวิทยาลัยเกิททิงเงิน (University of Göttingen) โดยวางแผนให้เรียนในสาขาเทววิทยาเพื่อที่พอเรียนจบแล้วจะได้เป็นบาทหลวงตามที่พ่อตั้งใจเอาไว้ แต่ที่มหาวิทยาลัยแห่งนี้มีสุดยอดนักคณิตศาสตร์คนสำคัญของโลกคือ Carl Friedrich Gauss ซึ่งตอนนั้นมีอายุ 70 ปีแล้ว เมื่อรีมันน์ได้เข้าฟังเลคเชอร์ของ Gauss โดยเฉพาะเรื่องวิธีกำลังสองน้อยที่สุด (method of least squares) เขาประทับใจมากและตัดสินใจเปลี่ยนมาเรียนวิชาคณิตศาสตร์แทนหลังจากได้รับการยินยอมจากพ่อ ปี 1847 รีมันน์ย้ายไปเรียนที่มหาวิทยาลัยเบอร์ลินและนี่นั่นเขาได้เรียนกับอาจารย์คณิตศาสตร์ชื่อดังหลายคน รวมทั้ง Carl Jacobi, Lejeune Dirichlet, และ Gotthold Eisenstein
รีมันน์เรียนอยู่ที่มหาวิทยาลัยเบอร์ลินนาน 2 ปีก่อนจะกลับมาเรียนต่อระดับปริญญาเอกที่มหาวิทยาลัยเกิททิงเงินโดยมี Carl Friedrich Gauss เป็นอาจารย์ที่ปรึกษา วิทยานิพนธ์ปริญญาเอกของเขาสร้างความประทับใจให้กับ Gauss อย่างมากถึงกับชื่นชมว่ามีคุณค่าสูงส่งเกินมาตรฐานของวิทยานิพนธ์ระดับปริญญาเอกเพราะผลงานนี้ได้ทำให้เกิดองค์ความรู้ใหม่มากมาย เช่น Riemann Surfaces, Theory of Holomorphic Functions และ Topology รีมันน์ได้รับปริญญาเอกสาขาคณิตศาสตร์ในปี 1851 ขณะมีอายุ 25 ปี
วิทยานิพนธ์ปูทางทฤษฎีสัมพัทธภาพ
ถึงแม้ว่ารีมันน์เรียนจบระดับปริญญาเอกแล้วแต่เขายังต้องทำวิทยานิพนธ์ระดับศาสตราจารย์ที่เรียกว่า Habilitation ซึ่งต้องทำด้วยตัวเองโดยไม่มีอาจารย์ที่ปรึกษาให้ผ่านก่อนถึงจะมีคุณสมบัติครบที่จะได้เป็นอาจารย์ในมหาวิทยาลัย ปี 1853 Gauss แนะนำเขาให้ทำวิทยานิพนธ์นี้ในเรื่องพื้นฐานของเรขาคณิต รีมันน์ใช้เวลาหลายเดือนในการพัฒนาทฤษฎีใหม่เกี่ยวกับรูปทรงเรขาคณิตที่ไม่ถูกจำกัดอยู่แค่เพียง 3 มิติ วิทยานิพนธ์ของเขาเสร็จในปี 1854 และเขาได้เลคเชอร์ครั้งแรกในหัวข้อ “On the hypotheses which underlie geometry” ซึ่งถือกันว่าป็นการบรรยายที่น่าทึ่งและมองการณ์ไกลที่สุดครั้งหนึ่งในประวัติศาสตร์คณิตศาสตร์
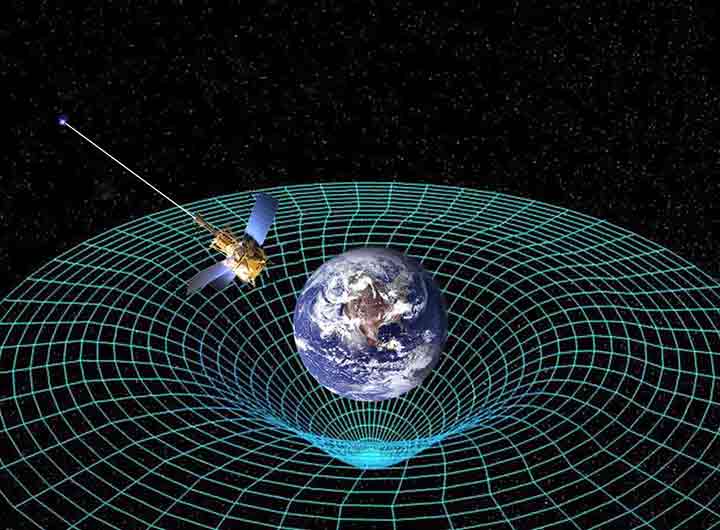
รีมันน์ได้คิดค้นเรขาคณิตเชิงอนุพันธ์ (Differential geometry) สาขาใหม่เรียกว่า Riemannian geometry ซึ่งเป็นรากฐานของเรขาคณิตสมัยใหม่ส่วนใหญ่ แนวคิดของรีมันน์ทำให้เรขาคณิตนอกระบบยูคลิด (Non-Euclidean geometry) ที่ริเริ่มโดย Carl Friedrich Gauss เมื่อหลายสิบปีก่อนมีความก้าวหน้าครั้งใหญ่ รูปทรงเรขาคณิตของรีมันน์สามารถมีมิติได้อย่างไม่จำกัดและเป็นรากฐานของเรขาคณิตสี่มิติของปริภูมิ – เวลา (space time) ที่ Albert Einstein นำไปใช้ศึกษาความสัมพันธ์ของอวกาศ แรงโน้มถ่วง มวล และเวลาสร้างเป็นทฤษฎีสัมพัทธภาพทั่วไปในปี 1915 จนกลายเป็นทฤษฎีฟิสิกส์ที่ยิ่งใหญ่ที่สุดในประวัติศาสตร์ ดังนั้นการที่จะเข้าใจทฤษฎีสัมพัทธภาพทั่วไปจำเป็นต้องเข้าใจเรขาคณิตของรีมันน์เสียก่อน
สมมติฐานของรีมันน์ที่รอคนเก่งพิสูจน์
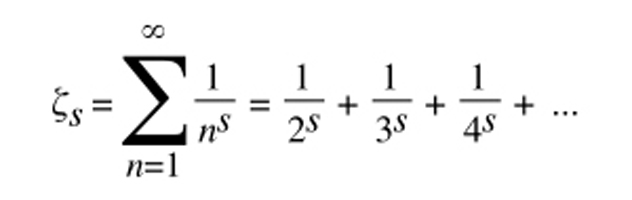
รีมันน์ทำงานเป็นอาจารย์ที่มหาวิทยาลัยเกิททิงเงินและได้รับการแต่งตั้งเป็นหัวหน้าแผนกคณิตศาสตร์ของมหาวิทยาลัยในปี 1859 ปีเดียวกันนั้นเองเขาได้เสนอฟังก์ชันหนึ่งซึ่งมีโดเมนเป็นจำนวนเชิงซ้อนเรียกว่า Riemann zeta function และตั้งสมมุติฐานว่าคำตอบที่ทำให้ค่าของฟังก์ชันนี้เท่ากับศูนย์คือจำนวนเต็มคู่ลบ (-2, -4, -6, …) กับจำนวนเชิงซ้อนที่จะต้องมีส่วนจริง (real part) เท่ากับ ½ เท่านั้นโดยที่เขาไม่ได้ทำบทพิสูจน์เอาไว้ นับจากปี 1859 จนกระทั่งถึงทุกวันนี้ก็ยังไม่มีใครสามารถพิสูจน์สมมติฐานนี้ได้ โจทย์นี้จึงเป็นโจทย์คณิตศาสตร์ที่ยากที่สุดโจทย์หนึ่งของโลกและทำให้รีมันน์มีชื่อเสียงเป็นที่รู้จักในวงกว้างมากกว่าผลงานอื่นๆ
ดาฟิด ฮิลแบร์ต (David Hilbert) นักคณิตศาสตร์ชื่อดังอีกคนหนึ่งถึงกับบอกว่าถ้าเขานอนหลับไปหลายศตวรรษแล้วตื่นขึ้นมา คำถามแรกที่เขาจะถามผู้คนรอบข้างคือมีใครพิสูจน์สมมติฐานของรีมันน์ (The Riemann Hypothesis) ได้แล้วบ้าง ถึงวันนี้ถ้าใครพิสูจน์สมมติฐานนี้ได้ว่าจริงหรือไม่จริงเป็นผลสำเร็จสถาบัน Clay Mathematics Institute ก็จะมอบเงินรางวัล 1 ล้านเหรียญให้แก่ผู้นั้น ปัจจุบันนักคณิตศาสตร์ได้พบว่าเทคนิคการวิเคราะห์สมมติฐานของรีมันน์ สามารถนำไปใช้ในการแก้ปัญหาอื่นๆได้อีกหลายเรื่อง เช่น Quantum Chaos, Cryptography และ Network Design
ผลงานการคิดค้นและพัฒนาที่โดดเด่น

รีมันน์เรียนจบปริญญาเอกที่มหาวิทยาลัยเกิททิงเงินแล้วทำงานเป็นอาจารย์ที่นี่จนกระทั่งได้เป็นศาสตราจารย์ ตลอดระยะเวลาเกือบ 20 ปีที่เขาศึกษาและทำงานที่มหาวิทยาลัยแห่งนี้รีมันน์มีผลงานการคิดค้นและพัฒนาทางคณิตศาสตร์จำนวนมาก และต่อไปนี้คือส่วนหนึ่งของผลงานที่สำคัญและโดดเด่นของเขา
ด้านเรขาคณิต – เรขาคณิตแบบยุคลิดคือการศึกษาจุด เส้น และคุณสมบัติของรูปทรงเรขาคณิตบนพื้นที่ราบหรือบนกระดาษแผ่นเรียบ แต่รีมันน์ศึกษาคุณสมบัติทางเรขาคณิตเหล่านั้นบนพื้นผิวโค้งหรือบนกระดาษที่โค้งงอซึ่งมีความซับซ้อนและยุ่งยากกว่ามาก ผลงานของเขาทำให้เกิดความรู้และทฤษฎีใหม่หลายอย่าง ได้แก่ Riemannian geometry, Algebraic geometry, Complex manifold, Riemann surfaces และ Differential geometry ซึ่งสาขาวิชาคณิตศาสตร์เหล่านี้เป็นรากฐานของวิชาโทโพโลยีและยังคงถูกนำไปใช้ในการพัฒนาวิชาฟิสิกส์อีกด้วย โดยเฉพาะวิชา Differential geometry ที่มีส่วนสำคัญในการสร้างทฤษฎีสัมพัทธภาพทั่วไป
ด้านการวิเคราะห์จำนวนเชิงซ้อน – ผลงานของรีมันน์ได้วางรากฐานทางเรขาคณิตสำหรับการวิเคราะห์จำนวนเชิงซ้อนผ่านทาง Riemann surfaces และทฤษฎี Riemann mapping รวมทั้งผลงานที่ผ่านทาง Abelian functions, Theta functions และเทคนิคอื่นๆอีกหลายอย่าง
ด้านการวิเคราะห์จำนวนจริง – ในปี 1854 รีมันน์ได้คิดค้น Riemann integral ขึ้นทำให้เขากลายเป็นคนแรกที่กำหนดอินทิกรัลของฟังก์ชันหรือพื้นที่ใต้เส้นโค้งในช่วงที่กำหนด นอกจากนี้เขายังมีผลงานในด้านการวิเคราะห์จำนวนจริงผ่านทาง Fourier series, Hypergeometric differential equations อีกด้วย
ด้านทฤษฎีจำนวน – ผลงานที่โด่งดังที่สุดและมีอิทธิพลมากที่สุดในด้านนี้ของรีมันน์เป็นบทความเรื่อง prime-counting function ซึ่งในบทความนี้เขาได้เสนอสมมติฐานของรีมันน์ที่ยังคงเป็นโจทย์คณิตศาสตร์ที่ยากที่สุดโจทย์หนึ่งของโลกจนถึงปัจจุบัน
หนีไม่พ้นคำกล่าว “อัจฉริยะมักอายุสั้น”

แบร์นฮาร์ด รีมันน์ เป็นศาสตราจารย์คณิตศาสตร์ตั้งแต่อายุยังน้อย เป็นนักคณิตศาสตร์อัจฉริยะที่มีผลงานโดดเด่นมากเป็นที่ยอมรับอย่างกว้างขวาง ได้รับแต่งตั้งเป็นสมาชิกต่างชาติของราชสมาคมแห่งลอนดอน (Royal Society of London) และสภาวิจัยวิทยาศาสตร์ของฝรั่งเศส (French Academy of Sciences) เขาใช้ชีวิตอย่างเรียบง่าย แต่งงานกับ Elise Koch ตอนอายุ 35 ปี มีลูกสาวด้วยกัน 1 คน หลังแต่งงานไม่นานเขาเริ่มป่วยเป็นวัณโรค ช่วงหลังเขาไปที่อิตาลีบ่อยเพราะนอกจากจะได้ชื่นชมกับศิลปะที่เขาชอบแล้วอากาศที่อิตาลียังช่วยให้อาการป่วยของเขาบรรเทาลงด้วย รีมันน์เสียชีวิตที่อิตาลีในปี 1866 น่าเสียดายที่เขาอายุสั้นแค่เพียง 39 ปีมิฉะนั้นวิชาคณิตศาสตร์อาจมีความก้าวหน้ามากกว่านี้
ข้อมูลและภาพจาก wikipedia, famousscientists, britannica